同時與順序遊戲

有沒有辦法描述同時遊戲和順序遊戲之間的區別？我試圖描述一種情況，即玩家只能在不知道其他玩家在遊戲給定階段的行動的情況下採取行動（即在遊戲的任何階段採取的行動是同時發生的），但允許重複遊戲. 我讀過 Gibbons (1992)，但沒有比這更明智的了。

在標準博弈論中，同時博弈和順序博弈通過稱為“資訊集”的方式來區​​分。提到博弈論的起源（von Neumann 和 Morgenstern 1944），同時移動遊戲可以被認為是順序移動遊戲的特殊情況。在他們具有里程碑意義的工作中，vN-M 給出了一種明確的方法來建構同時移動版本的順序遊戲。對他們來說，每一局遊戲本質上都是一個順序移動遊戲。但這只是歷史。

從理論的角度來看，重要的是玩家在遊戲中做出決定時“知道”之前的動作。這種“玩家在採取行動之前擁有的資訊”的概念在通過資訊集的順序移動遊戲（及其遊戲樹）中具有特徵。

例如，考慮囚徒困境。但是假設它以兩種不同的方式順序播放：

1. 玩家 1 移動。玩家 2 學習玩家 1 的動作。玩家 2 移動。
2. 玩家 1 移動。玩家 2 不知道玩家 1 的動作，但知道玩家 1 已經移動。玩家 2 移動。

在大多數情況下，2.本質上是一個同時移動遊戲。

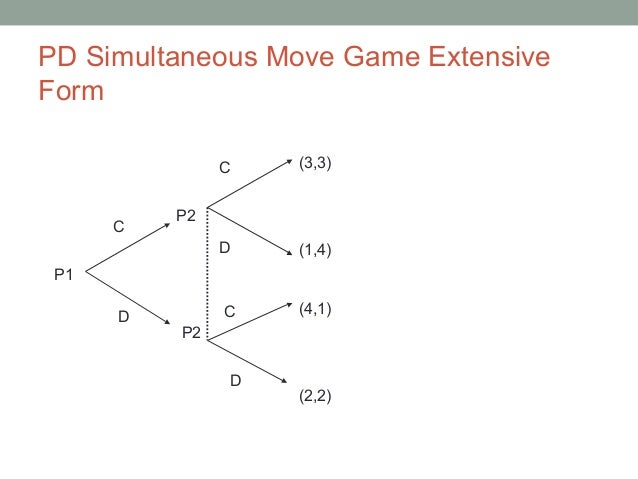
以下是我們通常如何以廣泛的形式表示同時移動遊戲。在上圖中，連接玩家 2 的兩個決策節點的虛線表示，在做出決定時，玩家 2 不知道她實際上在哪個節點。如果沒有虛線，則意味著玩家 2 知道她在哪個節點，因此了解了玩家 1 的選擇。在圖示的版本中，玩家 2 都知道如果她玩 C，她會得到 3 或 1，但僅此而已。請注意，這與我們在同時移動遊戲中的情況完全相同。然後很容易想像這種單發同時移動遊戲的重複版本。

在 GT 行話中，我們說這兩個連接的節點包含在同一個資訊集中。因此，資訊集是玩家無法區分的節點的集合。

引用自：https://economics.stackexchange.com/questions/43461